振動子は同期する - conserva’s diary

この記事はrogy Advent Calendar 2020 5日目の記事です。

勢いで登録したはいいんですが、全く書きたいことなくてどうしようかな～、というところで友人氏に要望はないか聞いてみたら、有難いことに答えてくれたので、フーリエ級数展開を線形代数っぽい視点から眺めてみるやつを書くか～と思ってちょっと調べてみたら、それっぽいちゃんとした記事(http://blog.physips.com/entry/fourier_orthogonal )が一瞬で出てきてしまったので、こちらのほうを参照頂ければと思います（完）。

さて、では今回は何を書くかというと、共通のガウスノイズを受けた振動子が同期していく様子を見てみたいと思います。（なんで？）

振動子が同期するとは

振動子というのは、読んで字のごとく振動するもののことです。メトロノームとかです。で、振動子が同期する、というのは、最初全然違うふるまいをしていた複数の振動子が、時間がたつにつれて同じようなふるまいをするようになることです。

メトロノームが同期する動画を見たことある人もいるんじゃないでしょうか。

www.youtube.com

あと、ホタルのチカチカとか。

www.youtube.com

これらは相互作用によって同期しているのですが、これから紹介するのは、少しだけ毛色の違う同期をします。

共通のガウスノイズを受ける振動子

はい。では、今回考えていく振動子に登場していただきます。じゃん

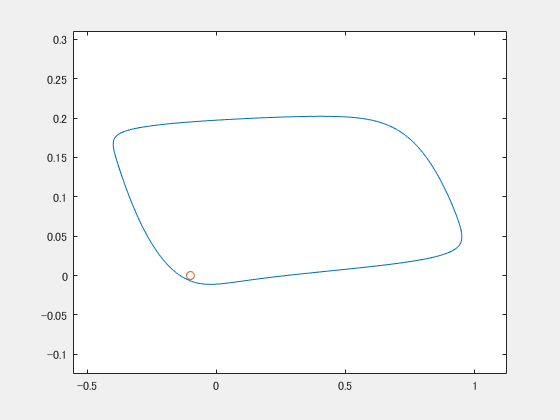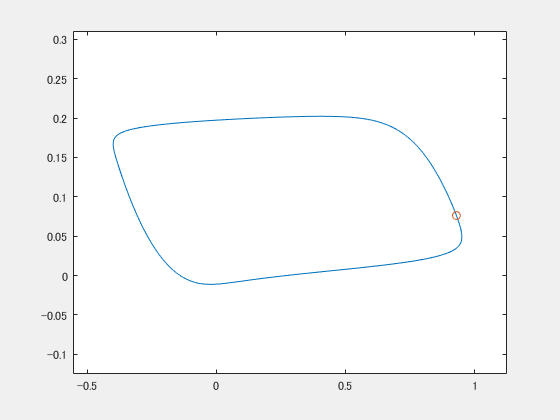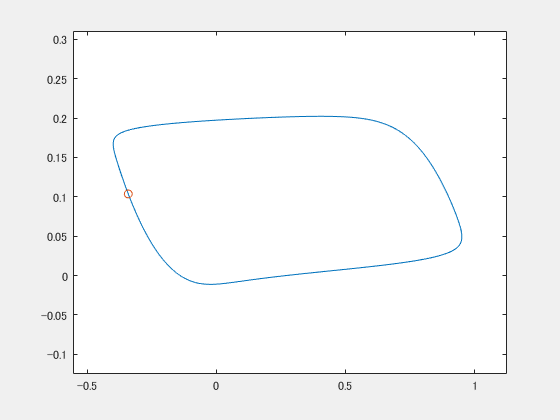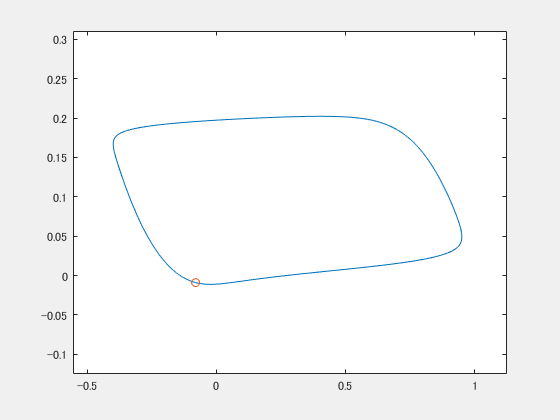
f:id:conserva:20201205002914g:plain — FitzHugh-南雲モデル

これはFitzHugh-南雲モデルというやつ（のパラメータを適当に設定したやつ）で、ごらんのとおり2次元平面をグルグル回ります。神経細胞の発火活動のモデルに使われたりするらしいです。で、違う初期値から始まるやつをもう一つ用意します。

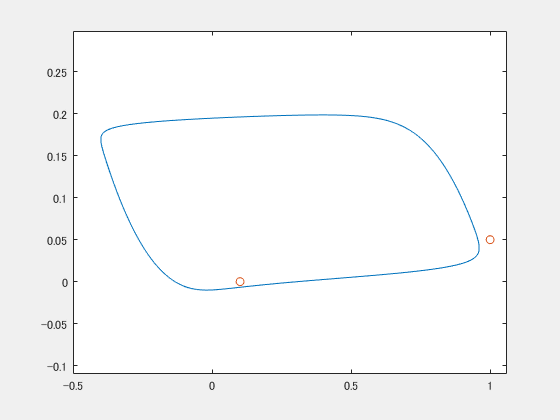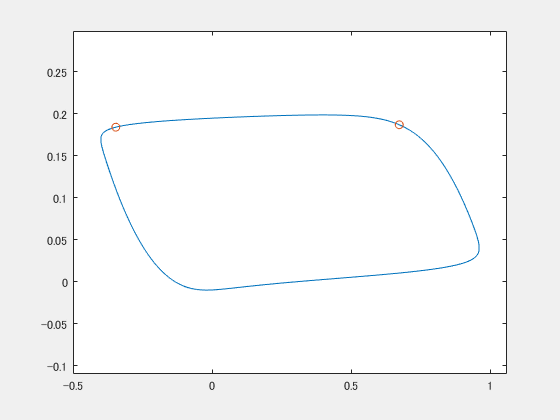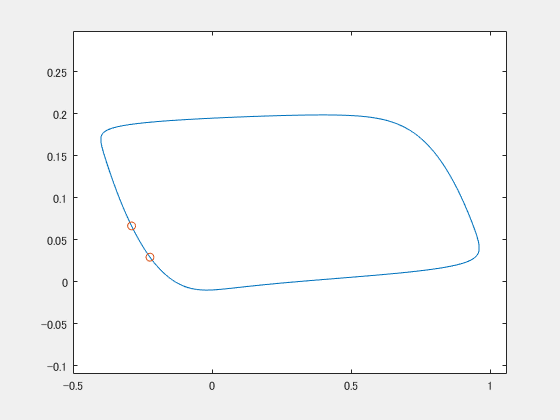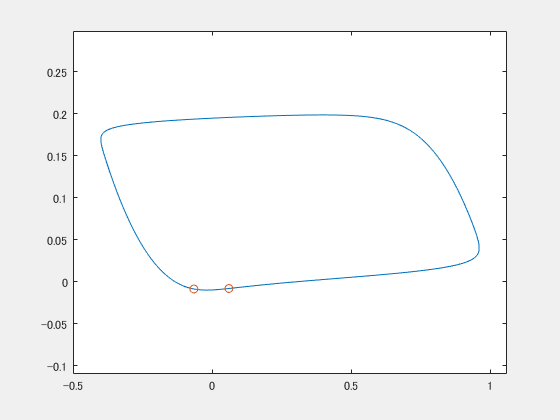
f:id:conserva:20201205134513g:plain — 2つの振動子たち

2つの振動子たちは今お互いに全然関係ない二人なので、バラバラです。ここに、共通した弱いノイズ（ガウスノイズ）を与えてみます。すると

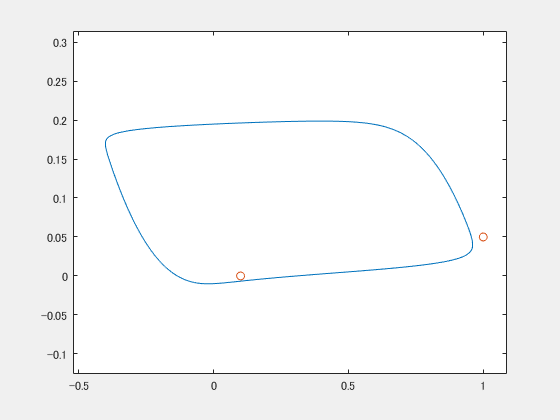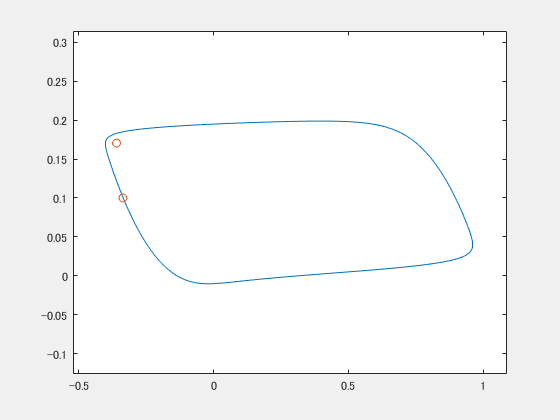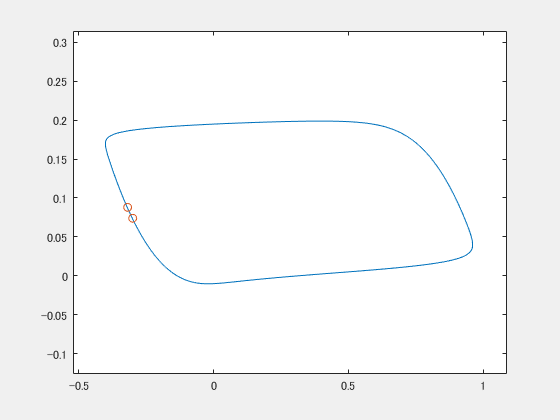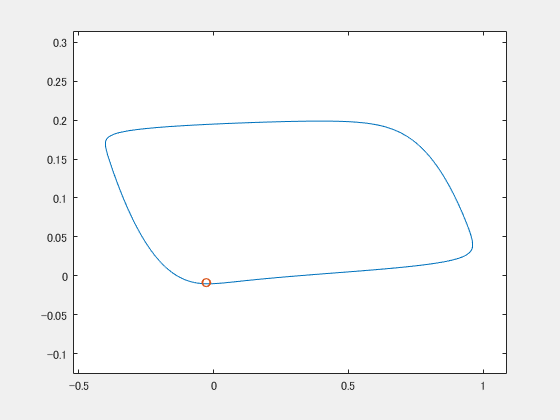
f:id:conserva:20201205134240g:plain — 同じノイズを受けたふたり

gifをループさせているので途中で分裂してるみたいに見えることに気づきましたが、ちゃんと最後同期してます。ちょっとプルプルしながら2つの〇が近づいていく様子がうかがえると思います。

2つの振動子は何ら相互作用をしていないのに、世界から同じ揺れを与えられたら同期してしまったわけです。

何で同期するのか

FitzHugh-南雲モデルに限らず、こういう風に放っておくとある軌道をグルグル回りだすような系はたくさんあります。わっかの上をグルグル回るので、振動子の状態をそのわっかの上の角度みたいなものを使って考えられそうです。その角度のようなものを位相(phase)と呼びます。2つの振動子のうち一つの位相を $\theta_1$ 、もう一つの位相を $\theta_2$ とし、 $\phi = \theta_1 - \theta_2$ とすると、 $\phi$ が0に収束すれば、同期したといえます。詳細については参考文献を後ろに乗せるので良ければ参照していただきたいですが、リアプノフ指数というのを（近似的に）計算することによって、共通のノイズを受ける同じ特性を持つ2つの振動子は同期する傾向を示すということが言えます。

使ったコード（MATLAB R2020b)

a = -0.1;                % FitzHugh-Nagumoのパラメータ
epsilon = 0.008;          % FitzHugh-Nagumoのパラメータ
gamma = 2;               % FitzHugh-Nagumoのパラメータ
varepsilon = 0.003;       % ノイズの強さ

dt = 0.01;
t = 0:dt:1000;
x0 = [0.1;0];           % 振動子1の初期値
y0 = [1;0.05];             % 振動子2の初期値
x = zeros(2,length(t)); % 振動子1の状態
y = x;                  % 振動子2の状態
x(:,1) = x0;
y(:,1) = y0;
z = x;   %軌道プロット用

for k = 2:length(t)
    noise = varepsilon*sqrt(dt)*randn*[1;1];            % [1;1]方向にノイズ
    x(:,k) = fitz(x(:,k-1),a,epsilon,gamma,dt) + noise; % Euler-Maruyama法
    y(:,k) = fitz(y(:,k-1),a,epsilon,gamma,dt) + noise;
    z(:,k) = fitz(z(:,k-1),a,epsilon,gamma,dt);
end
%plot(t,[x;y]); % 状態のプロット

%% plot(animation)
n = 48;
f = @(t)plot([x(1,round(n*t/dt)+1);y(1,round(n*t/dt)+1)]...
    ,[x(2,round(n*t/dt)+1);y(2,round(n*t/dt)+1)],'o');
plot(z(1,round(end/2):end),z(2,round(end/2):end)); % 軌道のわっかを表示
hold on
fanimator(f,'AnimationRange',[0 20])
axis([min(x(1,:))-0.1 max(x(1,:))+0.1 min(x(2,:))-0.1 max(x(2,:))+0.1])
hold off

%% playAnimation
playAnimation

function y = fitz(x,a,epsilon,gamma,dt)
    y = [x(1) + (-x(1)*(x(1)-1)*(x(1)-a)-x(2))*dt;x(2) + epsilon*(x(1)-gamma*x(2))*dt];
end

セクションごとに実行するとfigureが動き出します。

参考文献

ネットワーク・カオス- 非線形ダイナミクス,複雑系と情報ネットワーク - (情報ネットワーク科学シリーズ第 4巻), 中尾裕也 (著), 長谷川幹雄 (著), 合原一幸 (著), 電子情報通信学会 (監修) , Amazonのリンク